遺伝的アルゴリズムをGoで実装してみた

こんにちは！つるべーです！
最近は、進化計算と呼ばれるバイオミメティックな計算技法に興味を持っており、実装しながら勉強しています。
前回の記事では粒子群最適化（Particle Swarm Optimization: PSO）を実装しました。
今回は、遺伝的アルゴリズムという生物の進化の過程を模倣して作られた最適解探索アルゴリズムをGoでスクラッチで書いてみました。

遺伝的アルゴリズム（Genetic Algorithm: GA）

GAとは何か？という問いに対する答えとして、以下の一文が端的にその特徴を表していると思います。

生物進化における遺伝と適者生存による自然淘汰の仕組みをソフトウェア的に模すことで複雑な問題に対する最適解を探索する手法
引用：「遺伝的アルゴリズム（Genetic Algorithm）を始めよう！」

GAでは、問題に対する解を個体の染色体、解の構成要素を遺伝子として表現し、複数の個体を進化させて、より環境に適応できる個体を見つけることで最適解を導いていきます。その過程をフローチャートとしてまとめたものが以下になります。

コード

github.com

eago（イーゴ）という進化計算パッケージを鋭意開発中です！
ちなみに、Pythonで書かれたdeapという素晴らしいライブラリがあり、遺伝的アルゴリズムを始めとした様々な進化計算の手法が実装されています。

最適化問題を解いてみる

今回はAckley functionと呼ばれる関数の最小化問題を解いてみたいと思います。数式およびグラフは以下の通りです。グラフは左側が3Dに描いたもので、右側が2次元に写像したもの（左のグラフを上から見たもの）です。

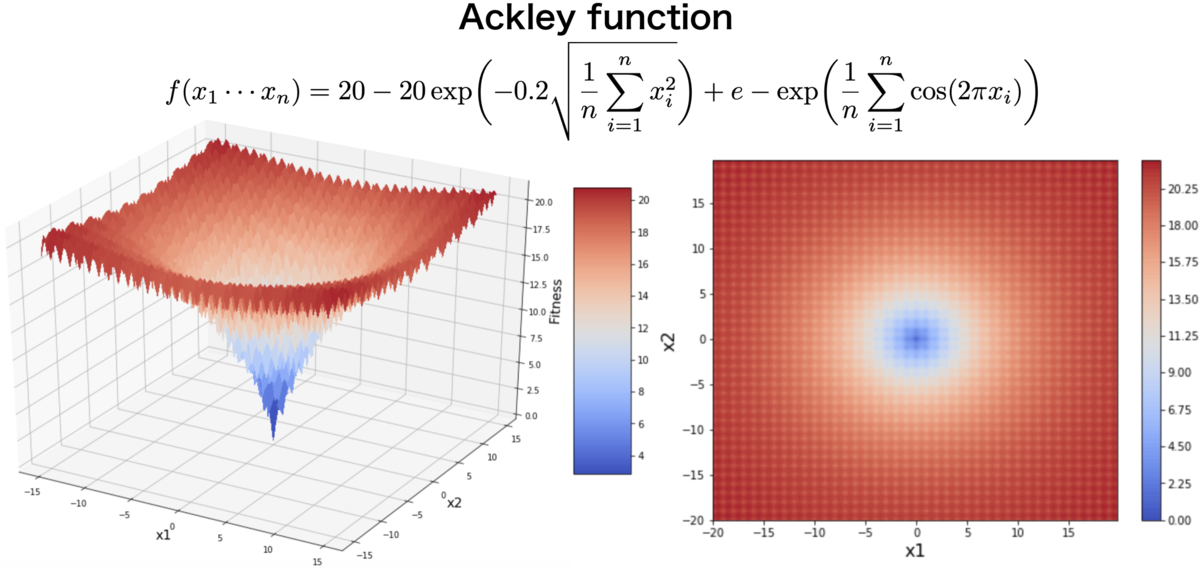
今回はの条件を採用しています。
Ackley functionは多峰性関数であり、多くの局所解をもつため、最適化アルゴリズムのベンチマーク関数として用いられることもあるようです。下のサイトに様々なベンチマーク関数が載っていて眺めるだけでも面白かったです。

Test functions for optimization - Wikipedia

グラフからわかるように、この関数はで最小値を取るため、今回の探索の目的は、を見つけることになります。

サンプルコードは以下の通りです。

package main

import (
    "github.com/tsurubee/eago"
    "log"
    "math"
)

type Variables []float64

func (V Variables) Initialization() eago.Genome {
    return Variables(eago.InitFloatVector(2, 32, -32))
}

func (V Variables) Fitness() float64 {
    return Ackley(V)
}

func (V Variables) Mutation() {
    eago.AddNormalFloat(V, 0.5)
}

func (V Variables) Crossover(X eago.Genome) eago.Genome {
    return Variables(eago.BLXalpha(V, X.(Variables), 0.3))
}

func Ackley(X []float64) float64 {
    a, b, c, d := 20.0, 0.2, 2*math.Pi, float64(len(X))
    var s1, s2 float64
    for _, x := range X {
        s1 += x * x
        s2 += math.Cos(c * x)
    }
    return -a*math.Exp(-b*math.Sqrt(s1/d)) - math.Exp(s2/d) + a + math.Exp(1)
}

func main() {
    var v Variables
    ga := eago.NewGA(eago.GAConfig{
        PopulationSize: 30,
        NGenerations:   20,
        CrossoverRate:  0.8,
        MutationRate:   0.01,
    })
    if err := ga.Minimize(v); err != nil {
        log.Fatal(err)
    }
}

コードの詳細については最後に補足します。
上のコードをmain.goとして以下のように実行します。

$ go run main.go
Generation   1: Fitness=11.208 Solution=[-4.501 0.087]
Generation   2: Fitness=10.001 Solution=[-3.592 -0.833]
Generation   3: Fitness=9.165 Solution=[-3.841 -0.960]
Generation   4: Fitness=5.747 Solution=[-1.426 -0.235]
Generation   5: Fitness=4.258 Solution=[-0.824 0.380]
Generation   6: Fitness=2.797 Solution=[-0.843 -0.011]
Generation   7: Fitness=2.605 Solution=[-0.955 -0.030]
Generation   8: Fitness=2.605 Solution=[-0.955 -0.030]
Generation   9: Fitness=2.604 Solution=[-0.925 0.016]
Generation  10: Fitness=2.604 Solution=[-0.925 0.016]
Generation  11: Fitness=2.479 Solution=[-0.346 -0.054]
Generation  12: Fitness=1.216 Solution=[-0.184 -0.006]
Generation  13: Fitness=0.615 Solution=[-0.111 -0.001]
Generation  14: Fitness=0.501 Solution=[-0.096 -0.007]
Generation  15: Fitness=0.267 Solution=[-0.055 0.024]
Generation  16: Fitness=0.056 Solution=[0.010 -0.014]
Generation  17: Fitness=0.056 Solution=[0.010 -0.014]
Generation  18: Fitness=0.053 Solution=[-0.005 -0.015]
Generation  19: Fitness=0.031 Solution=[0.010 0.003]
Generation  20: Fitness=0.013 Solution=[-0.000 0.004]

出力結果を見てみると、世代数が大きくなるにつれて、Fitnessが、パラメータの解がに収束しようとしているため、うまく探索できていることがわかります。

最後に、今回用いたコードとアルゴリズムの補足をしておきます。

実装とアルゴリズムの補足

Genomeインターフェース

実装では、下記のようなGenomeインターフェースを定義しており、上記のサンプルコードのVariablesはGenomeインターフェースを満たすように各メソッドを実装しています。

type Genome interface {
    Initialization() Genome
    Fitness() float64
    Mutation()
    Crossover(Genome) Genome
}

このように実装した理由は、eagoを使う側で自由に独自に実装した選択や交叉などの手法を組み込めるようにするためです。できればメジャーな手法については全てeago側に実装して、特殊なケース以外は全てeagoに実装されたメソッドを呼び出すだけで事足りるようにしていきたいと思っています。

実数値遺伝的アルゴリズム（Real coded GA）

今回の最適化では、解表現に浮動小数点数を用いており、実数値GAと呼ばれる手法を実装しました。
GAにおいては、各遺伝子を0か1で表現したバイナリエンコーディングが最も一般的な解表現だと思います。このような解の表現の仕方により、探索過程の各ステップ（選択・交叉・突然変異）で用いる手法も大きく異なってきます。
それぞれのステップにおいて、今回用いた手法を説明します。

選択

今回用いている選択の手法は、トーナメント法と呼ばれるものです。
任意のn個の個体を組にして、それらの中で最も適応度が高いものを選択するという手法になります。
他の手法として、ルーレット法やランキング法などがあります。

交叉

交叉にはブレンド交叉（BLX-α）という実数値GA特有の手法を用いました。
BLX-αについては下のサイトがわかりやすく解説されていました。

実数型GAに於ける交叉法の改良

親となる2個体によってできる長方形を一定数倍引き伸ばした長方形で囲まれる範囲内でランダムに次世代の個体が生成されます。

突然変異

突然変異として、個体の各遺伝子に任意の確率で一様乱数を加算するようなものを実装しました。一般的に突然変異は、局所解に陥ることを防ぐために取り入れられます。

さいごに

GAは、解の表現の仕方や、選択・交叉・突然変異など各遺伝子操作に様々な手法が提案されていて、何を使うかは問題を解く側に委ねられており、以前実装したPSOと比べて、非常に自由度が高いという印象を受けました。なので、GAの理論や実装をまだまだ深掘りしながら楽しめそうです！
今後は、処理の並列化や多目的最適化への拡張などを中心に勉強していきたいと思っています。