　異常検知にもいろいろアプローチがあります。例えば、距離に基づくアプローチ、統計学に基づくアプローチ、機械学習に基づくアプローチなどが挙げられます。今回はその中でも統計学に基づくアプローチについて書きます。統計学に基づく異常検知のアプローチは統計的異常検知とも呼ばれます。
　統計的異常検知とは、データの生成機構が確率モデル（確率分布）で表現できると仮定した場合の異常検知の方法論です。これはデータから得られる「知識」を確率モデルという形で表現していると捉えることもできます。

統計的異常検知の手順

統計的異常検知は基本的に以下の3ステップからなります。

観測データからデータ生成の確率モデルを学習
さらに細かく分けると以下の２ステップあります。
① 未知パラメータを含む確率分布を仮定
② データから未知パラメータを推定
学習したモデルを基に、データの異常度合いをスコアリング（異常度の定義）
閾値の設定

今回は、統計的異常検知の中でも最も基本的な、1次元正規分布に基づく異常検知について、上記の３ステップを一つずつ解説していきます。

データの準備

用いるデータは、Rのデータセットにある「Davisデータ」というもので、200人の性別、測定した身長・体重、および自己申告の身長・体重が記録されています。 https://vincentarelbundock.github.io/Rdatasets/datasets.html

　前提として、今回扱うデータは測定した体重だけであり、１変数です。すなわち確率的に揺らぐ値（確率変数）が1種類だけ存在するということです。もちろん、これから示す方法論は、多変量にも拡張できますが、1変数から始めた方が数式が追いやすいです。
　横軸を標本番号、縦軸を体重として、データを可視化したものが以下になります。

f:id:hirotsuru314:20170919224410p:plain:w550

　また、このデータのヒストグラムは下のようになります。

f:id:hirotsuru314:20170919224425p:plain:w550

　どちらもパッと見で異常値が見つけられると思います。このデータの異常判定をしたいとき、「120kg以上は異常だ！」としてif文で検知するのは簡単ですが、その120kgという値には何の根拠もなく、説得力に欠けると思います。これを統計学を駆使して、より客観的な水準で判定してやろうというのが今回の話です。
観測データがN個あるとき、データをまとめて $D$ という記号で表すとします。

$\displaystyle D= \{x_1,x_2,...,x_N\}$

ここで、観測データが多次元の場合は、 $x$ が列ベクトルとして表されます。また、このデータの中には異常な観測データが含まれていないか、含まれていたとしてもその影響は無視できると仮定します。
これから前述した統計的異常検知の3ステップに沿って話を進めていきます。

1. 観測データからデータ生成の確率モデルを学習する

① 未知パラメータを含む確率分布を仮定
　上記のヒストグラムによると、体重データの分布は若干左右非対称ではありますが、おおむね山の形になっています。そこで、それぞれの観測データ $x$ が平均 $\mu$ 、分散 $\sigma^2$ の正規分布に従うと仮定します。

$\displaystyle N(x|\mu, \sigma^2)=\frac{1}{\sqrt{2\pi \sigma^2}}\exp{\left\{-\frac{(x-\mu)^2}{2\sigma^2}\right\}}$

② データから未知パラメータを推定
　正規分布に含まれているパラメータは平均 $\mu$ 、分散 $\sigma^2$ の二つです。言い換えると、この二つのパラメータが決定すると、分布の形が一意に決まるということです。これらのパラメータを観測データから推定します。パラメータ推定には最尤推定を用います。最尤推定は、「観測データが得られる確率」をパラメータの関数とみなした尤度関数を最大化するようにパラメータを決定する推定法です。

$\displaystyle \begin{eqnarray} p(D|\mu, \sigma^2) & = & \prod_{n=1}^N N(x_n|\mu, \sigma^2) \\ & = & \prod_{n=1}^N\frac{1}{\sqrt{2\pi \sigma^2}}\exp{\left\{-\frac{(x_n-\mu)^2}{2\sigma^2}\right\}} \\ & = & (2\pi \sigma^2)^{-\frac{N}{2}}\exp{\left\{-\frac{1}{2\sigma^2}\sum_{n=1}^{N}(x_n-\mu)^2 \right\}} \end{eqnarray}$

ここで、計算の都合上、尤度関数の自然対数をとった対数尤度関数を最大化します。対数は単調増加であるため、尤度関数の最大化は対数尤度関数の最大化と同値です。
$\beta=\frac{1}{\sigma^2}$ とした場合、対数尤度尤度関数は、

$\displaystyle \ln p(D|\mu, \sigma^2)=\frac{N}{2}\ln \beta - \frac{N}{2}\ln 2\pi - \frac{\beta}{2}\sum_{n=1}^{N}(x_n-\mu)^2$

これを最大化するパラメータを求めるため、 $\mu$ と $\beta$ でそれぞれ偏微分してゼロと等置します。

$\displaystyle \frac{\partial}{\partial \mu}\ln p(D|\mu, \sigma^2)=0 \tag{1}$

$\displaystyle \frac{\partial}{\partial \beta}\ln p(D|\mu, \sigma^2)=0 \tag{2}$

$(1)$ より

$\displaystyle \begin{eqnarray} \frac{\partial}{\partial \mu}\ln p(D|\mu, \sigma^2) & = & \beta\sum_{n=1}^{N}(x_n-\mu) \\ & = & \beta \biggl(\sum_{n=1}^{N}x_n-N\mu\biggl) \\ \end{eqnarray}$

$\displaystyle ∴　\mu=\frac{1}{N}\sum_{n=1}^{N}x_n$

$(2)$ より

$\displaystyle \frac{\partial}{\partial \beta}\ln p(D|\mu, \sigma^2) = \frac{N}{2\beta}-\frac{1}{2}\sum_{n=1}^{N}(x_n-\mu)^2$

$\displaystyle ∴　\sigma^2=\frac{1}{N}\sum_{n=1}^{N}(x_n-\mu)^2$

　平均・分散の推定値は私たちがよく知っている平均・分散の定義そのものだということがわかると思います。これらの結果は、平均・分散の推定値として、観測データの標本平均・標本分散を採用することを意味しています。また、推定した平均・分散にはデータからの推定値であることを明示するため「^（ハット）」をつけます。
したがって、学習モデル（予測分布） $p(x|\hat{\mu}, \hat{\sigma^2})$ が得られたことになります。
ここで、 $\hat{\mu}$ と $\hat{\sigma^2}$ はデータセットが与えられると一意に決まります。（普通にデータの平均・分散を出すだけです。）

2. 学習したモデルを基に、データの異常度合いをスコアリング（異常度の定義）

　一般に、異常度の定義として、負の対数尤度を採用されることが多いです。（これは情報理論におけるシャノン情報量と呼ばれるものです）
新たな観測値 $x'$ に対する異常度 $a(x')$ は、

$\displaystyle \begin{eqnarray} a(x') & = & -\ln p(x'|\hat{\mu}, \hat{\sigma^2}) \\ & = & -\ln \biggl[\frac{1}{\sqrt{2\pi \hat{\sigma}^2}}\exp{\left\{-\frac{(x'-\hat{\mu})^2}{2\hat{\sigma}^2}\right\}} \biggr] \\ & = & \frac{1}{2}\ln (2\pi \hat{\sigma}^2)+\frac{1}{2\hat{\sigma}^2}(x'-\hat{\mu})^2 \end{eqnarray}$

第1項は観測データ $x'$ に依存しないので無視します。全体に2をかけると、異常度は、

$\displaystyle a(x')=\biggl(\frac{x'-\hat{\mu}}{\hat{\sigma}}\biggl)^2$

という形で表されます。
分子 $(x'-\hat{\mu})$ は観測データの標本平均からのずれの大きさを表しており、ずれが大きくなると異常度が大きくなります。
分母は $\hat{\sigma}$ であり、標準偏差で割ることで、もともとばらつきの大きいものは多少のずれでも多めに見るようになっており、異常度の表現として非常に直感に近い形になっていることがわかります。

3. 閾値の設定

　異常度が決まると、それに閾値を設定することで異常判定をすることができます。閾値は経験に基づき主観的に決める方法もありますが、できるだけ客観的基準に基づいて決めるのが望ましいです。
　ホテリング理論は、観測データが正規分布に従うことを仮定した下で異常検知を行う非常に有名な古典理論であり、広く応用されています。ホテリング理論が有効な理由の一つは、異常度が従う確率分布を、明示的に導くことができる点です。異常度の確率分布が既知であれば、それに基づいて閾値を設定するのは容易です。例えば、「正常には1パーセント未満でしか起こらないくらい稀な値だから、きっと正常ではないだろう」という論理になります。つまり、パーセント値により異常判定を行うことができるようになります。
　ホテリング理論によると異常度 $a(x’)$ はデータ数Nが十分に大きい時、自由度1のカイ二乗分布に従うということが数学的に証明できます。
　下のグラフは自由度1のカイ二乗分布の確率密度関数です。

f:id:hirotsuru314:20170919224519p:plain:w550

　ここで、カイ二乗分布とは、 $Z_1,Z_2,...Z_n$ を独立な標準正規分布 $N(0, 1)$ に従う確率変数としたとき、

$\displaystyle \chi^2=Z_1^2+Z_2^2+...+Z_n^2$

とすると、確率変数 $\chi^2$ が従う確率分布を自由度 $n$ のカイ二乗分布といいます。
（異常度がカイ二乗分布に従うことの数学的な証明は難解なため避けますが、Nが十分に大きいとき、標本平均・標本分散は母平均・母分散に近づき、 $a(x’)$ が「確率変数から母平均を引いて、母標準偏差で割ったもの」すなわち標準正規分布 $N(0, 1)$ の2乗に従うようになるからだと考えてよいのだと思います）

Pythonによる実践

　これまで説明した1次元正規分布に基づく異常検知をPythonで実装したいと思います。
　ここで、入力として、データと異常度の閾値(%)を与えると、出力として、異常値とそのインデックス番号を返す関数を作りたいと思います。

import numpy as np
from scipy import stat

def hotelling_1d(data, threshold):
    """
    Parameters
    ----------
    data : Numpy array
    threshold : float

    Returns
    -------
    List of tuples where each tuple contains index number and anomalous value.
    """
    #Covert raw data into the degree of abnormality
    avg = np.average(data)
    var = np.var(data)
    data_abn = [(x - avg)**2 / var for x in data]

    #Set the threshold of abnormality
    abn_th = stats.chi2.interval(1-threshold, 1)[1]

    #Abnormality determination
    result = []
    for (index, x) in enumerate(data_abn):
        if x > abn_th:
            result.append((index, data[index]))
    return result

　この関数に引数のdataとして、200人の体重データを渡すと以下のように、

hotelling_1d(data, 0.01)
#-> [(11, 166), (20, 119)]

　異常値として2点返ってきます。
　結果を可視化すると下のようになります。縦軸は異常度です。グラフ内の赤の破線は異常度の閾値です。（プログラム中の「abn_th」の値に対応）

f:id:hirotsuru314:20170919224604p:plain:w550

　プログラムを見てもわかりますが、結局ほぼデータの平均と分散を計算して、ちょろっと異常度に変換するとできてしまいます。カイ二乗分布の確率密度関数は非常に複雑ですが、SciPyを用いるとその積分値は簡単に出せます。

ホテリング理論の課題

　ホテリング理論では、観測データ同士が互いに独立で、それぞれが単一の正規分布に従っていると仮定していますが、それは非常に強い制約と言えます。したがって、下記のようなデータには適用は困難です。

１. 複数のモードがあるような複雑な系への適用
　例えば、複数のピークを持ち、単一の正規分布で仮定できないような場合です。

２. 値が動的に変化する時系列データへの適用が困難
　正規分布を仮定するということは、データの分布がひと山でだいたい安定しているとみなしいますが、平均の値が揺らぐようなデータもあります。いわゆる時系列データと呼ばれる類のものですが、そのようなデータにホテリング理論は適用が困難です。
　時系列データの異常検知についてはまた別の機会に書きたいと思います。

参考文献

入門機械学習による異常検知―Rによる実践ガイド

作者: 井手剛
出版社/メーカー: コロナ社
発売日: 2015/02/19
メディア: 単行本
この商品を含むブログ (4件) を見る

現在日本語で読める異常検知の本ではおそらく一番やさしく、読みやすい。時系列データの異常検知についても載っている。

2017-09-02

Python製の対話的可視化ライブラリBokehを使ってみる

Python データサイエンス

　Pythonには様々なデータ可視化ライブラリがありますが、私は最近Bokehというライブラリを知って、その便利さにハマってます！今回はBokehの簡単なチュートリアル的な内容を書きたいと思います。

Bokehとは？

　Bokehって何？の答えを知るには下記の公式ページを見るのが一番良いと思います。ただ、日本語版はないようです。

bokeh.pydata.org

　Bokehの特徴をいくつか挙げると、

対話的な可視化ができる（対話的って何？というのは後で書きます）
斬新奇抜なグラフが描ける
ビッグデータをリアルタイムで処理できる
グラフを作るためにHTML・CSS・JavaScriptを書く必要がない

といった感じです。
ちなみにBokehの主な開発者は、有名なPythonパッケージであるAnacondaを開発している人たちのようです。
実際の開発者によるBokehについてのプレゼン資料がslideshareにあり、非常に面白いです。

Hassle Free Data Science Apps with Bokeh Webinar

Bokehを触って見る

　それでは実際にBokehを触ってみようと思います。

#Importing libraries
from bokeh.plotting import figure
from bokeh.io import output_file, show

#prepare data
x = [1,2,3,4,5]
y = [6,7,8,9,10]

#prepare the output file
output_file("Line.html")

#create figure
fig = figure()
fig.line(x, y)
show(fig)

こんな短いコードで対話的なグラフが描けます。今回データについてはコードに直書きしています。こちらを実行すると（コマンドラインでpython file名を叩くと）、ブラウザ上にページが立ち上がり、下のようにグラフが描画されています。

f:id:hirotsuru314:20170902100536p:plain

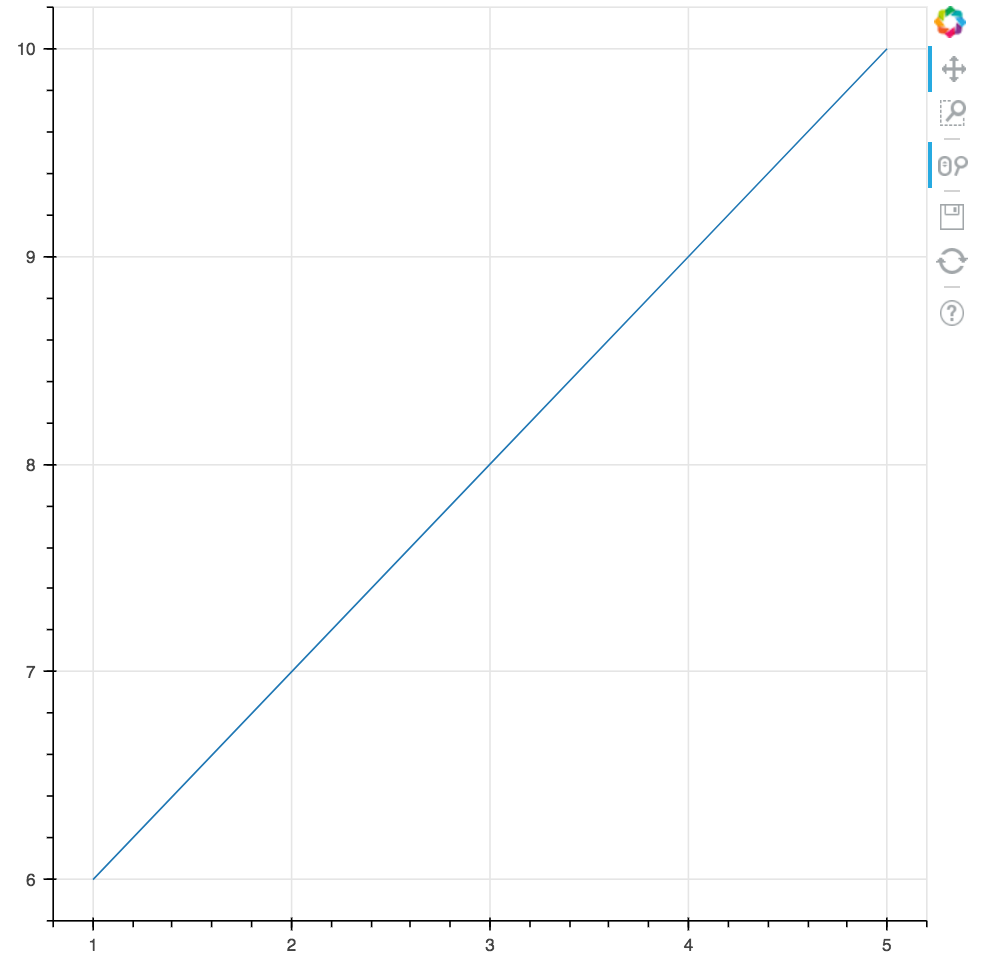
これを右上にドラッグすると、

f:id:hirotsuru314:20170902100545p:plain

スクロールすると、

f:id:hirotsuru314:20170902100559p:plain

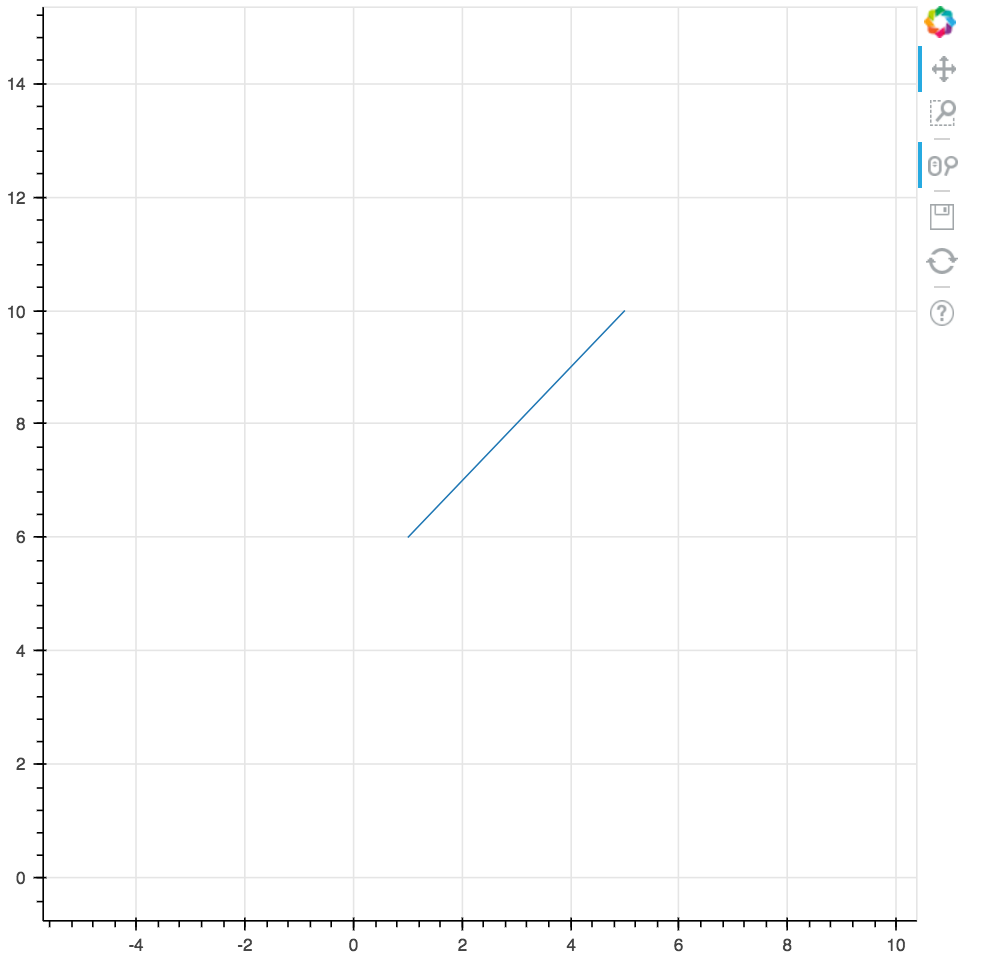
対話的とはこういうことで、ユーザーの操作に対して即座に動きが返ってくる仕組みになっています。ぜひ実際にやってみてグラフをグリグリできる楽しさを味わってみてください！（動画を載せようと思ったのですが、パッと調べた感じYouTube等を使う方法しかなく、画像にしました。わかりづらくてすみません、いい方法あれば教えてください^^;）

上記のコードの中の

output_file("Line.html")

の部分で、Bokehが生成してくれたHTMLファイルも出力するようにしているので、出力されたHTMLの中をみてみましょう。

<!DOCTYPE html>
<html lang="en">
    <head>
        <meta charset="utf-8">
        <title>Bokeh Plot</title>

<link rel="stylesheet" href="https://cdn.pydata.org/bokeh/release/bokeh-0.12.2.min.css" type="text/css" />

<script type="text/javascript" src="https://cdn.pydata.org/bokeh/release/bokeh-0.12.2.min.js"></script>
<script type="text/javascript">
    Bokeh.set_log_level("info");
</script>
        <style>
          html {
            width: 100%;
            height: 100%;
          }
          body {
            width: 90%;
            height: 100%;
            margin: auto;
          }
        </style>
    </head>
    <body>

        <div class="bk-root">
            <div class="plotdiv" id="a7161ecc-bd75-43de-9089-247eb36da918"></div>
        </div>

        <script type="text/javascript">
            Bokeh.$(function() {
            Bokeh.safely(function() {
                var docs_json = {"ceb05a6f-303a-42ec-8fe1-717a3c3ba468":{"roots":{"references":[{"attributes":{"overlay":{"id":"c8df6c4b-20d9-4d00-ab91-8696851c6517","type":"BoxAnnotation"},"plot":{"id":"89f15627-1da2-4be9-8b49-7242d04f73e2","subtype":"Figure","type":"Plot"}},"id":"fe131afa-6cb9-4027-8e5e-81f50a7f7c2f","type":"BoxZoomTool"},{"attributes":{"formatter":{"id":"e9a2431f-b252-4bc6-86ca-98dd06d792ca","type":"BasicTickFormatter"},"plot":{"id":"89f15627-1da2-4be9-8b49-7242d04f73e2","subtype":"Figure","type":"Plot"},"ticker":{"id":"1e5e43c3-495b-471d-a871-7f085567f5fe","type":"BasicTicker"}},"id":"272fbeb6-e972-4283-94f3-c5c01022aaf3","type":"LinearAxis"},{"attributes":{"callback":null},"id":"50aa3059-7d61-402f-96d9-e51c4d7b4ab4","type":"DataRange1d"},{"attributes":{"bottom_units":"screen","fill_alpha":{"value":0.5},"fill_color":{"value":"lightgrey"},"left_units":"screen","level":"overlay","line_alpha":{"value":1.0},"line_color":{"value":"black"},"line_dash":[4,4],"line_width":{"value":2},"plot":null,"render_mode":"css","right_units":"screen","top_units":"screen"},"id":"c8df6c4b-20d9-4d00-ab91-8696851c6517","type":"BoxAnnotation"},{"attributes":{"plot":{"id":"89f15627-1da2-4be9-8b49-7242d04f73e2","subtype":"Figure","type":"Plot"},"ticker":{"id":"6ccb7a55-c184-446a-b680-3135cd27775d","type":"BasicTicker"}},"id":"1844c54b-118b-452b-83bd-ed647412592f","type":"Grid"},{"attributes":{"data_source":{"id":"a13993f5-d7b0-4174-88bb-b90f2e6c1412","type":"ColumnDataSource"},"glyph":{"id":"bafa0919-8be4-4742-8c66-2805ce1f9da4","type":"Line"},"hover_glyph":null,"nonselection_glyph":{"id":"29ac1919-026e-4ed7-a866-b13a07c96bfe","type":"Line"},"selection_glyph":null},"id":"a7d00cc9-6e84-413a-a3e9-e1eb94796522","type":"GlyphRenderer"},{"attributes":{"formatter":{"id":"f521c266-6f21-4f57-8c1d-5d8196ce5fa2","type":"BasicTickFormatter"},"plot":{"id":"89f15627-1da2-4be9-8b49-7242d04f73e2","subtype":"Figure","type":"Plot"},"ticker":{"id":"6ccb7a55-c184-446a-b680-3135cd27775d","type":"BasicTicker"}},"id":"449bd4d4-7483-4290-88a0-f1593170ee1d","type":"LinearAxis"},{"attributes":{"plot":{"id":"89f15627-1da2-4be9-8b49-7242d04f73e2","subtype":"Figure","type":"Plot"}},"id":"d64e9c84-783f-4d2c-9254-46a5b09d79e8","type":"PanTool"},{"attributes":{"callback":null},"id":"963839b2-34d1-414c-be56-c84bdb1ef5cc","type":"DataRange1d"},{"attributes":{"plot":{"id":"89f15627-1da2-4be9-8b49-7242d04f73e2","subtype":"Figure","type":"Plot"}},"id":"9a747cea-226e-4006-b86a-6d6b186765f1","type":"WheelZoomTool"},{"attributes":{"plot":{"id":"89f15627-1da2-4be9-8b49-7242d04f73e2","subtype":"Figure","type":"Plot"}},"id":"8109f175-be7e-4f0f-b4b3-3d0bc4762177","type":"HelpTool"},{"attributes":{"line_alpha":{"value":0.1},"line_color":{"value":"#1f77b4"},"x":{"field":"x"},"y":{"field":"y"}},"id":"29ac1919-026e-4ed7-a866-b13a07c96bfe","type":"Line"},{"attributes":{},"id":"e9a2431f-b252-4bc6-86ca-98dd06d792ca","type":"BasicTickFormatter"},{"attributes":{"dimension":1,"plot":{"id":"89f15627-1da2-4be9-8b49-7242d04f73e2","subtype":"Figure","type":"Plot"},"ticker":{"id":"1e5e43c3-495b-471d-a871-7f085567f5fe","type":"BasicTicker"}},"id":"386d29c4-a962-48fe-815f-18666d39826c","type":"Grid"},{"attributes":{},"id":"f9cb966f-a936-4979-9465-afee14f8f21d","type":"ToolEvents"},{"attributes":{},"id":"6ccb7a55-c184-446a-b680-3135cd27775d","type":"BasicTicker"},{"attributes":{"plot":{"id":"89f15627-1da2-4be9-8b49-7242d04f73e2","subtype":"Figure","type":"Plot"}},"id":"2de10c54-d536-4ec1-9904-d39d9c57d1cb","type":"SaveTool"},{"attributes":{"callback":null,"column_names":["x","y"],"data":{"x":[1,2,3,4,5],"y":[6,7,8,9,10]}},"id":"a13993f5-d7b0-4174-88bb-b90f2e6c1412","type":"ColumnDataSource"},{"attributes":{"active_drag":"auto","active_scroll":"auto","active_tap":"auto","tools":[{"id":"d64e9c84-783f-4d2c-9254-46a5b09d79e8","type":"PanTool"},{"id":"9a747cea-226e-4006-b86a-6d6b186765f1","type":"WheelZoomTool"},{"id":"fe131afa-6cb9-4027-8e5e-81f50a7f7c2f","type":"BoxZoomTool"},{"id":"2de10c54-d536-4ec1-9904-d39d9c57d1cb","type":"SaveTool"},{"id":"5dc6dca4-c75b-428e-a030-60e291cd1162","type":"ResetTool"},{"id":"8109f175-be7e-4f0f-b4b3-3d0bc4762177","type":"HelpTool"}]},"id":"c1e5b658-fb25-422c-947d-a9e05d1babb9","type":"Toolbar"},{"attributes":{"line_color":{"value":"#1f77b4"},"x":{"field":"x"},"y":{"field":"y"}},"id":"bafa0919-8be4-4742-8c66-2805ce1f9da4","type":"Line"},{"attributes":{},"id":"1e5e43c3-495b-471d-a871-7f085567f5fe","type":"BasicTicker"},{"attributes":{},"id":"f521c266-6f21-4f57-8c1d-5d8196ce5fa2","type":"BasicTickFormatter"},{"attributes":{"below":[{"id":"449bd4d4-7483-4290-88a0-f1593170ee1d","type":"LinearAxis"}],"left":[{"id":"272fbeb6-e972-4283-94f3-c5c01022aaf3","type":"LinearAxis"}],"renderers":[{"id":"449bd4d4-7483-4290-88a0-f1593170ee1d","type":"LinearAxis"},{"id":"1844c54b-118b-452b-83bd-ed647412592f","type":"Grid"},{"id":"272fbeb6-e972-4283-94f3-c5c01022aaf3","type":"LinearAxis"},{"id":"386d29c4-a962-48fe-815f-18666d39826c","type":"Grid"},{"id":"c8df6c4b-20d9-4d00-ab91-8696851c6517","type":"BoxAnnotation"},{"id":"a7d00cc9-6e84-413a-a3e9-e1eb94796522","type":"GlyphRenderer"}],"title":{"id":"57403a00-d3e6-47c5-a4e0-0fb338855f24","type":"Title"},"tool_events":{"id":"f9cb966f-a936-4979-9465-afee14f8f21d","type":"ToolEvents"},"toolbar":{"id":"c1e5b658-fb25-422c-947d-a9e05d1babb9","type":"Toolbar"},"x_range":{"id":"50aa3059-7d61-402f-96d9-e51c4d7b4ab4","type":"DataRange1d"},"y_range":{"id":"963839b2-34d1-414c-be56-c84bdb1ef5cc","type":"DataRange1d"}},"id":"89f15627-1da2-4be9-8b49-7242d04f73e2","subtype":"Figure","type":"Plot"},{"attributes":{"plot":{"id":"89f15627-1da2-4be9-8b49-7242d04f73e2","subtype":"Figure","type":"Plot"}},"id":"5dc6dca4-c75b-428e-a030-60e291cd1162","type":"ResetTool"},{"attributes":{"plot":null,"text":null},"id":"57403a00-d3e6-47c5-a4e0-0fb338855f24","type":"Title"}],"root_ids":["89f15627-1da2-4be9-8b49-7242d04f73e2"]},"title":"Bokeh Application","version":"0.12.2"}};
                var render_items = [{"docid":"ceb05a6f-303a-42ec-8fe1-717a3c3ba468","elementid":"a7161ecc-bd75-43de-9089-247eb36da918","modelid":"89f15627-1da2-4be9-8b49-7242d04f73e2"}];

                Bokeh.embed.embed_items(docs_json, render_items);
            });
        });
        </script>
    </body>
</html>

データはJSON形式に変換されて、JavaScriptに渡されています。このようにHTML・CSS・JavaScriptとして出力されるため、Webとの親和性も高く、FlaskやDjangoを使ったアプリへの組み込みも容易にできます。

さいごに

　Bokehの公式ページにあるギャラリーには超ファンシーなグラフたちがあり、実際に触れるようになっています。えっほんとにこんなことまでできるの？っていうものもあるので、ぜひ見てみてください！

https://bokeh.pydata.org/en/latest/docs/gallery.html

2017-08-13

Pythonで状態空間モデルを使う（StatsModels）

Python

今回は、代表的な時系列モデルである状態空間モデルをPythonで使う方法を書いていきます。先日、『時系列データ分析とPython』という記事を書きましたが、今回はその内容の実装部分にあたります。（状態空間モデルって？という方はぜひ前回の記事を見て下さい！）

blog.tsurubee.tech

用いるデータは、時系列のデータセットとして大変有名な『各年ごとのナイル川流量』のデータです。

f:id:hirotsuru314:20170702224936p:plain

このデータは今回用いる統計ライブラリであるStatsModelsの中のデータセットにも入っています。

statsmodels/nile.csv at master · statsmodels/statsmodels · GitHub

さっそくですが、このデータに状態空間モデルをあてはめてみます。

import pandas as pd
from datetime import datetime
import matplotlib.pyplot as plt
%matplotlib inline
import statsmodels.api as sm

#日付形式で読み込む
dateparse = lambda dates: pd.datetime.strptime(dates, '%Y') 
#CSV読み込み
data = pd.read_csv('nile.csv', index_col='year', date_parser=dateparse)

# ローカルレベルモデルによる状態推定
model = sm.tsa.UnobservedComponents(data, 'local level')
result = model.fit()
fig = result.plot_components()

f:id:hirotsuru314:20170813224510p:plain

　状態空間モデルの実質的なコードは最後のたった3行だけです。
　黒線のObserved（観測データ）に対して、青線が推定した状態（潜在変数）になります。
　今回あてはめたモデルは状態空間モデルの中でも一番単純なローカルレベルモデルと呼ばれるモデルです。このモデルはランダムウォークプラスノイズモデルとも呼ばれ、ランダムウォークで推移している潜在変数（真の状態）に、何かしらのノイズ（不規則要素）がのっかって、観測データが得られるといったシンプルなモデルです。
　このようにStatsModelsを使うと、とても短いコードで状態空間モデルを使うことができます。下記のリンクがStatsModelsの状態空間モデル部分のリファレンスです。

statsmodels.tsa.statespace.structural.UnobservedComponents — statsmodels 0.9.0 documentation

今回の例では

model = sm.tsa.UnobservedComponents(data, 'local level')

のように第2引数として'local level'を渡していますが、上記リンクのStatsModelsリファレンスに記載のとおり、ここが実際にどのようなモデルを用いるかを決めます。したがって、例えば引数に、‘local linear trend’を渡せばローカルレベルモデルに線形のトレンドを加えたモデルに拡張することができます。また、『seasonal=12』といった引数を渡せば月の季節性成分を入れることも容易にできます。
　実際のモデリングのプロセスでは、データをよく再現するモデルを見つけるため、様々な要素（トレンド成分、季節性成分など）を入れながら、モデルの試行錯誤を行います。その上で参考となる指標も、下記のように簡単にsummaryとして出すことができます。

print(result.summary())

f:id:hirotsuru314:20170813230712p:plain

　推定したパラメータだけでなくLjung-Box検定などの検定の結果もまとめて出すことができます。
　今回の状態推定はStatsModelsのUnobservedComponentsの中のfit関数を呼び出しただけです。公式リファレンスによると、『Fits the model by maximum likelihood via Kalman filter.』と書いてあり、裏側ではカルマンフィルタによる最尤推定を行なっているようです。

参考　

カルマンフィルタ ―Rを使った時系列予測と状態空間モデル― (統計学One Point 2)

作者: 野村俊一
出版社/メーカー: 共立出版
発売日: 2016/09/08
メディア: 単行本
この商品を含むブログを見る

　本のタイトルは『カルマンフィルタ』とピンポイントですが、状態空間モデルの基礎からカルマンフィルタ、粒子フィルタによる非線形非ガウス状態空間モデルまで幅広く学べる良書です。

2017-07-02

時系列データ分析とPython

Python

　先日、『時系列データ分析とPython』というタイトルでLTをしたので、そのときのスライドをこちらに載せておきます。

時系列データ分析とPython from Hirofumi Tsuruta

www.slideshare.net

　LTで話したとは言っても、私自身、数ヶ月前まで時系列データなんてほとんど触ったことなくて、ここ最近興味を持ち、勉強を始めました。スライドには最小限のことしか載せてないので、こちらに内容の補足を書いていきます。

時系列データの取り扱いは難しい

　時系列データとは、時間の推移ととともに観測されるデータのことです。私たちの身の回りには時系列データが溢れています。例えば、気温・雨量といった気象データも時系列データですし、株価や為替といった金融データも時系列データです。
　これらのデータは時間の推移とともに観測されるというのはもちろんですが、多くの場合で時間依存性を持ちます。例えば、株価の場合、前日の値動きはどうか、上昇傾向なのか、下落傾向なのかが重要だというのはイメージしやすいかと思います。この時間依存性がデータ分析の際にやっかいな存在です。
　多くのデータ分析手法において、「それぞれのデータを独立と仮定する」という仮定を置いた上で分析を行うケースがよくあります。しかし、時間依存性を持っていると、この仮定が成り立たず、取り扱いが非常に難しくなります。
　下のグラフは、ナイル川流量の各年ごとのデータを表しており，有名な時系列データセットです。

f:id:hirotsuru314:20170702224936p:plain

Pythonの統計ライブラリStatsModels

　Pythonで統計モデリングしようと思うと、StatsModelsを使うことになるかと思います。

StatsModels: Statistics in Python — statsmodels 0.9.0 documentation

　StatsModelsは数多くの統計モデリング手法を提供してくれるライブラリです。一般化線形モデル(generalized linear model; GLM)に始まり、今回使った状態空間モデルもStatsModelsを使えば、簡単に構築できます。ちなみに状態空間モデルについてはこちらに書いてあります。

statsmodels.tsa.statespace.structural.UnobservedComponents — statsmodels 0.9.0 documentation

状態空間モデル

　状態空間モデルでは、データの変動の原因を「水準の変化」と「観測誤差」という二つに分けて考えます。イメージ図は下記のような感じです。 f:id:hirotsuru314:20170702225141p:plain

　状態空間モデルを使えば、欠測データや時変回帰係数、さらに多変量への拡張まで状態空間の枠組みの中で、柔軟にモデリングが行えます。状態空間モデルについては、下記リンクと、その関連ページを読むと、だいたい感覚はつかめると思います。

状態空間モデル | Logics of Blue

　今回、状態推定はStatsModelsのUnobservedComponentsの中のfit関数を呼び出しただけです。公式リファレンスによると、『Fits the model by maximum likelihood via Kalman filter.』と書いてあり、裏側ではカルマンフィルタによる最尤推定を行なっているようです。状態空間モデルにおけるパラメータ推定法は下記の記事がよくまとまっていて、参考になります。カルマンフィルタ・粒子フィルタ・マルコフ連鎖モンテカルロ法（Markov chain Monte Carlo methods; MCMC）について整理してあります。

状態空間モデルの推定方法の分類 | Logics of Blue

実装部分についても書きました（2017年8月13日更新）

blog.tsurubee.tech

参考書　

現場ですぐ使える時系列データ分析 ~データサイエンティストのための基礎知識~

作者: 横内大介,青木義充
出版社/メーカー: 技術評論社
発売日: 2014/02/18
メディア: 単行本（ソフトカバー）
この商品を含むブログ (6件) を見る

　おそらく現時点で日本語で読める時系列解析の本ではこの本が一番やさしいと思います。ゼロから始めるには最適だと思います。時系列データとは？に始まり、自己相関・定常過程・単位根過程・ホワイトノイズ・ランダムウォークといった時系列解析でよく出てくる用語を理解するのに非常に役立ちます。実践の部分は、GARCHモデルがメインで、状態空間モデルについては取り扱っていません。サンプルコードはRです。

データ解析のための統計モデリング入門――一般化線形モデル・階層ベイズモデル・MCMC (確率と情報の科学)

作者: 久保拓弥
出版社/メーカー: 岩波書店
発売日: 2012/05/19
メディア: 単行本
購入: 16人クリック: 163回
この商品を含むブログ (29件) を見る

　時系列うんぬんの前に統計モデリングやるなら結局みどり本を読まなきゃですね。私もいつもかなり勉強させていただいているTJOさんの記事にもみどり本程度の統計モデリングの知識は必要なスキルセットとしてあげられてました。

データサイエンティストもしくは機械学習エンジニアになるためのスキル要件とは（2017年夏版） - 六本木で働くデータサイエンティストのブログ

2017-05-28

【統計】モデル選択とAIC

　最近、社内で統計モデリングのバイブル本である『データ解析のための統計モデリング入門』の勉強会を行っており、第４章の部分を担当したので、その際の資料をこちらに載せておきます！

データ解析のための統計モデリング入門4章 from Hirofumi Tsuruta

www.slideshare.net

　第４章は『GLMのモデル選択ーAICとモデルの予測の良さー』という内容で、ざっと中身を説明すると、統計モデルを構築する際に、どのようにして良いモデルを選択するか、について書かれています。ありがちな間違いとして、手持ちのデータへのあてはまりの良さ（誤差が小さい）を基準としがちですが、それは正しくありません。その理由は主に２つあるとか思います。
　１つ目は、データへのあてはまりの良さはモデルを複雑にすることでいくらでも改善できる点です。これは機械学習などで『過学習』と言われる状態で、たまたま手元に持ち合わせているデータだけに適応しているだけに過ぎないかもしれません。
　２つ目は、そもそも統計モデルを作る目的ってなんだっけ？ということを考えると、手持ちのデータを再現することではなく、真の統計モデルを推定すること、ひいては、データが観測される現象の背後にある「しくみ」の特定です。それらを理解することで、次に得られるデータがどういうものかを予測したいというわけです。そして、この予測の良さを重視するモデル選択基準がAIC（Akaike’s information criterion）です。
　この『データ解析のための統計モデリング入門』という本はよく『みどり本』などと呼ばれており、かなり人気のある本らしいです。私も最近知って読んでいるのですが、かなりわかりやすくて感動してます！何かしらの分析したいデータをお持ちで、それを統計モデルにあてはめてみたいという方はぜひ読んでみてください！

データ解析のための統計モデリング入門――一般化線形モデル・階層ベイズモデル・MCMC (確率と情報の科学)

作者: 久保拓弥
出版社/メーカー: 岩波書店
発売日: 2012/05/19
メディア: 単行本
購入: 16人クリック: 163回
この商品を含むブログ (29件) を見る

2017-05-05

消防士からエンジニアに転職して半年が経ちました

　こんにちは！私事ですが、エンジニアに転職して半年が経ちました！以前は消防士という全く違う世界で仕事をしており、プログラムの経験もほとんどないままエンジニアになりましたが、なんとか普通に仕事ができるようになってきました！
　今回は、私が転職して半年で学んだことや、これからできるようになりたいことなどを書いていきます。今後エンジニアへの転職を考えている人やプログラムを勉強中の方々の参考になればと思います。

転職の話はこちらに書きました↓　 blog.tsurubee.tech

今なにをやっているか
経験ゼロから転職してどうだったか
半年でできるようになったこと
半年で読んでよかった本
これからできるようになりたいこと

今なにをやっているか

　2016年11月に経験ゼロからシステム開発会社に拾っていただきました。私が勤めている会社は主にECサイトの受託開発・保守等を行なっています。私は現在、ECサイトのレコメンドエンジンの開発・保守を行なっています。「これを買った人はこれも買っています」みたいなやつです。また、それに加えてここ数ヶ月は、ECサイトのデータ分析の仕事もしています。
　開発言語は、Pythonを使っており、データ分析の仕事ではSQLをゴリゴリ書いています。また、レコメンドエンジンをやらせてもらったことをきっかけに機械学習に興味を持ち、業務外で自分で学習モデルを組んで、画像認識や文書分類などもやっています。あとは、機械学習をやる上で理論まで理解しようとすると、かなり数学の力が必要だなって実感して、微分積分・線形代数・最適化数学なども勉強中です！

経験ゼロから転職してどうだったか

　私がエンジニアになったときのスキルセットは、Rubyが少し書ける、Excelが少し使えるくらいでした。そんな中で、初日からいきなり案件にジョインさせて頂いて、わからないことの連続でした。Linuxサーバーをコマンドラインから操作してみると、「cd ディレクトリ名」で移動して・・むっ、戻れない。。上の階層への戻り方を知らず、「cd /」でルートに戻ってました。笑
　そんなこんなで周りの方にも迷惑をかける日々でしたが、会社に入る前に独学で本を読みながら勉強しているのとは比較にならないスピードで成長できたと思います。やはり、実際に手を動かして慣れるのが一番だと実感しました。なので、私は、本当にエンジニアになりたいなら「まだスキル全然ないしなー」とか考える前に未経験でも拾ってもらえる会社を探して、実際に現場に飛び込むのが良いと思っています。

半年でできるようになったこと

　この半年でできるようになったことを挙げるとざっとこんな感じです。（それぞれできるといってもレベルは低いですが。。）

プログラム

　プログラムに関しては、現在仕事でPythonを使っていることもあり、Pythonがそこそこ書けるようになりました。むしろ今Python以外、書ける言語がないのでちょっとやばいかもって思ってます。笑
　言語もさることながら、その背後にあるオブジェクト指向についても勉強しました。クラスとかインスタンスとか最低限知識がないとオブジェクト指向型のプログラムを書くとき・読むときにかなり支障がでるので、そこはかなり重要と思います。

数学・統計学

　私は一応理系の大学を出ましたが、久しぶりに数式に触れるとすっかり忘れており、記憶から完全に葬り去られていることに気づきました。。なので数学は一通り勉強しなおしました。やったこととしては、主に微分・積分や線形代数あたりです。
　また、機械学習の勉強をしていると、「統計的機械学習」とか「ベイズ統計学」といったフレーズが出てきて、ベイズってなに？？というレベルだったので一通り勉強しました。本気で統計学をやろうと思うと、かなり数学を使うので、統計学を学ぶには同時並行で数学を学ぶことになるでしょう。

機械学習

　機械学習については主要なアルゴリズムがだいたいわかる程度にはなりました。また、実際にTensorFlowやKerasなどのライブラリを使ってニューラルネットのモデルが組み、文書分類などを行ったりしました。現在、機械学習はライブラリが充実しているので、初学者が実際にモデルを組んでデータを扱うまでの壁はほとんど感じられないと思います。ただ、実際に自分が直面している課題を機械学習を導入することで、解決するところまでいくにはかなり壁があるなーと思いました。現在壁を乗り越えるため、理論をしっかり理解することが必要だと思うので、真剣に勉強中です。

データ分析

　おそらく、ここ半年で一番成長したと思えるのはSQLです。仕事でかなりSQLを書く機会があり、最初はSELECT文とかさえ知らなかった私が、今ではテーブルの結合や集計なども使いこなせるようになり、ときには数百行にまたがるSQL文を書いてデータの集計・分析をし、BIツールで可視化といったことをやっています。
　あと最近は、R言語も使い始めました！もともとPythonが多少書けるのでRは使う気はなかったのですが、データ分析系の本を買うと、サンプルコードがRというケースが多すぎるので、心が折れて使い始めました・・笑　

半年で読んでよかった本

　半年でいろんな本を読みましたが、この本はまじで読んでよかった！っていう本がいくつかありますので紹介したいと思います。

ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装

作者: 斎藤康毅
出版社/メーカー: オライリージャパン
発売日: 2016/09/24
メディア: 単行本（ソフトカバー）
この商品を含むブログ (18件) を見る

　もはや今更どうこういうレベルではないくらい多くの方に読まれているかと思いますが、ディープラーニング学ぶならまじで最高の1冊です。ただ、幅広い機械学習の分野の中で、良くも悪くもディープラーニングのみに特化した本です。Pythonでライブラリを使わず、ニューラルネットワークを実装するのでかなり力がつくと思います。

ITエンジニアのための機械学習理論入門

作者: 中井悦司
出版社/メーカー: 技術評論社
発売日: 2015/10/17
メディア: 単行本（ソフトカバー）
この商品を含むブログ (2件) を見る

　上のオライリーの本ではディープラーニングしか取り扱ってないのと対照的に、この本ではディープラーニング以外の主要なアルゴリズムはだいたい押さえています。ざっと挙げると、最小二乗法、最尤推定法、パーセプトロン、ロジスティック回帰、k平均法、EMアルゴリズム、ベイズ推定、といった感じです。本書は機械学習の入り口的な本としての位置付けですが、本中のコラムにはけっこうガチな数学の議論をしてます。２章の最小二乗法でいきなり「ヘッセ行列」とか出てきたときは、「まじか！」と思いました。数学が不得意な方はコラム抜きで読んでも、主要アルゴリズムの概論的なものがだいたいわかるかと思います。

プログラミングのための線形代数

作者: 平岡和幸,堀玄
出版社/メーカー: オーム社
発売日: 2004/10/01
メディア: 単行本
購入: 27人クリック: 278回
この商品を含むブログ (90件) を見る

　数学系の本を読んで初めておもしろい！と感動を覚えました。本書では冒頭に「行列は写像だ！」と連呼しているのですが、正直最初はなにを言っているんだろう、行列ってあの数字が表みたいに並んだやつよね？って思っていました。しかし今では、行列が写像にしか見えません。笑　行列を見た瞬間、これは5次元から3次元への線形変換だな、とか、これは時計回りに90度回転しているなっとか、行列の見方が一気に変わりました。これ、機械学習ではめちゃくちゃ大事なことです！　同著者が「プログラミングのための確率統計」という本も出していて読みましたが、なんか説明が回りくどく私には合いませんでした。

これなら分かる最適化数学―基礎原理から計算手法まで

作者: 金谷健一
出版社/メーカー: 共立出版
発売日: 2005/09/01
メディア: 単行本
購入: 29人クリック: 424回
この商品を含むブログ (42件) を見る

　数学の本でもう一冊読んでよかった本を挙げるなら、この本です。この本を読むことで機械学習の「学習」部分で使う最適化アルゴリズムへの理解が深まります。同著者の「これなら分かる応用数学教室」もかなりいい本でしたが、機械学習をやるなら最適化数学の方が直結するような気がします。

図解・ベイズ統計「超」入門あいまいなデータから未来を予測する技術 (サイエンス・アイ新書)

作者: 涌井貞美
出版社/メーカー: SBクリエイティブ
発売日: 2013/12/17
メディア: 新書
この商品を含むブログ (15件) を見る

　ベイズってなに？って言う状態から、ベイズってこういうことね！って言う状態までに最短で行くには最適の本です。私はベイズ統計学という名前を聞いたことがない状態で、この本を読み始めましたが、ベイズの考え方はだいたいわかりました。ただ、この本を読んでも、ベイズをつかって何かしよう！というレベルにはいかないです。本当に導入部分を知るための１冊です。　

これからできるようになりたいこと

　これからできるようになりたいことを3つほど挙げましたが、今まさに本気で勉強中です。ここらへんをブログでアウトプットしていきたい・・

機械学習の理論を本気で理解する

　前述しましたが、機械学習をただ使えるのと、理論を理解して使いこなすとの差はすさまじく大きいと思います。機械学習の理論を学ぶのに最適な本は何かと調べているとだいたいこの本にぶち当たります。　

パターン認識と機械学習上

作者: C.M.ビショップ,元田浩,栗田多喜夫,樋口知之,松本裕治,村田昇
出版社/メーカー: 丸善出版
発売日: 2012/04/05
メディア: 単行本（ソフトカバー）
購入: 6人クリック: 33回
この商品を含むブログ (20件) を見る

　かの有名なPRMLです。（プレモルとか呼ばれてるらしい）
　ただ、ぶっちゃいきなりやるのはかなり無謀だと感じました。なので、いろんな方のブログで、PRML挑戦の前段階で位置付けられているはじめてのパターン認識を勉強中です。
　今年中には、PRMLの方に手を出したい・・。

統計学を使いこなせるようになりたい

　最近、データ分析の仕事をしていると、統計学の大事さを痛感します。統計学を知らないと分析の結果を出しても、その根拠を示せないからです。また、統計学を学ぶ過程で、かなり数学が必要になるので、都度都度、数学も補いながらやると、一石二鳥かなって思ってます。ディープラーニングをやるだけなら、微分と線形代数くらいでいけるけど、ここに確率的な議論が入ると、積分もガンガン使うので、理論が飛躍的になるように思います。逆に言うと、非常に習得が難しい統計学をしっかり理解している人材ってあまりいないし、かなり貴重だと思います。なので、このあたりを攻めると他と差別化できそうな気がしてます。
　あと、統計モデリングとかできるようになりたいなって漠然と思い、みどり本を読み始めました。

データ解析のための統計モデリング入門――一般化線形モデル・階層ベイズモデル・MCMC (確率と情報の科学)

作者: 久保拓弥
出版社/メーカー: 岩波書店
発売日: 2012/05/19
メディア: 単行本
購入: 16人クリック: 163回
この商品を含むブログ (29件) を見る

まだ3章までしか読んでないですが、めちゃくちゃおもしろいです！　

英語が壁にならないようにする

　学生時代には英語をかなりしゃべる環境に身を置いており、そこそこ自信はあったのですが、それから消防士になり5年くらい全くしゃべってなかったので、本当に話せなくなってました。今でも、読むのにはほとんど苦労しないし、聞くのもだいたい何言っているかわかりますが、話すのが全然ダメになっているので、そこをなんとかしたいです。もともと英語を話すために英語を勉強するっていうのは嫌いで、英語はあくまでもツールの一つなので、勉強しないスタンスを貫いてきたのですが、それが障壁になり、チャンスを逃すようになるともったいないので、勉強を始めてみようと思います。
　とは言ったもののなにから始めてよいものか・・悩み中です。

Fire Engine

消防士→ITエンジニア→研究者

プログラマのための数学勉強会@福岡 #6に登壇しました

1次元正規分布に基づく異常検知の理論とPythonによる実装

はじめに

統計的異常検知の考え方

統計的異常検知の手順

データの準備

1. 観測データからデータ生成の確率モデルを学習する

2. 学習したモデルを基に、データの異常度合いをスコアリング（異常度の定義）

3. 閾値の設定

Pythonによる実践

ホテリング理論の課題

参考文献

Python製の対話的可視化ライブラリBokehを使ってみる

Bokehとは？

Bokehを触って見る

さいごに

Pythonで状態空間モデルを使う（StatsModels）

参考

時系列データ分析とPython

時系列データの取り扱いは難しい

Pythonの統計ライブラリStatsModels

状態空間モデル

実装部分についても書きました（2017年8月13日更新）

参考書

【統計】モデル選択とAIC

消防士からエンジニアに転職して半年が経ちました

今なにをやっているか

経験ゼロから転職してどうだったか

半年でできるようになったこと

プログラム

数学・統計学

機械学習

データ分析

半年で読んでよかった本

これからできるようになりたいこと

機械学習の理論を本気で理解する

統計学を使いこなせるようになりたい

英語が壁にならないようにする